【簡単】活性化関数の３つの目的！中間層と出力層で役割・違いを発見♪

ディープラーニングでは活性化関数を使用します。

『活性化関数の目的は、なんだろう？』

『中間層と出力層で活性化関数の役割は違うの？』

『それぞれの活性化関数の違いは何だろう？』

こんな疑問に答えます。

SE歴25年のオッサンが解説するぞい！

ＳＥおっさん

活性化関数の３つの目的！中間層と出力層の役割の違い

活性化関数には、以下の３つの役割があります。

１つ目は、どの層の活性化関数にも言える前提です。

正解値と出力値の誤差を勾配降下法で最小化する必要があります。

勾配降下法は微分の連鎖律を使用するため、活性化関数は微分ができる必要があるんです。
（ここでは勾配降下法の説明には触れません）

２つ目と３つ目は、中間層・出力層で活性化関数に求められる目的が異なります。

中間層の活性化関数の目的は、複雑な判定を可能にすることです。

複雑な判定は非線形関数の中間層を重ねることで実現できます。

つまり…

中間層の活性化関数は非線形関数であることが望ましい

ということです。

非線形関数とは、１次関数のような直線でない関数のことです。

指数関数などは非線形関数となります。

出力層の活性化関数の目的は、求められる出力の形にすることです。

問題であれば、数値

分類問題であれば、分類の確率

となります。

たろちゃん

回帰と分類の違いがワカラナイ

出力の形は、下記の例がイメージしやすいと思います。

↓こんな感じです。

回帰は数値、分類は確率になっていますね。

このように、出力層の活性化関数では、求められる出力の形にする必要がある訳です。

たろちゃん

あぁ、そゆこと！

中間層の活性化関数(非線形関数)と勾配消失問題

中間層では勾配消失問題を防ぐことができる非線形関数が望ましいです。

先日、僕はこんなツイートをしました。

活性化関数の中継ぎエースはRelu⚾️
シグモイド関数の微分は最大値が0.25だから
連鎖率の原理で微分した値が掛け算されると誤差がドンドン小さくなって、誤差修正しても学習効果が薄くなる
→勾配消失問題
Relu関数の微分はxが0より大きい限り、常に1だからOK
シグモイドはリリーフやな😁

— バリタス@ＡＩおっさん (@koisyo_ok) May 23, 2020

勾配消失問題

ディープラーニングでは誤差逆伝播法で勾配降下法を用いて誤差を修正することで学習していきます。
勾配消失問題とは誤差がドンドン小さくなって、誤差修正しても学習効果が薄くなる問題です。

例えば…

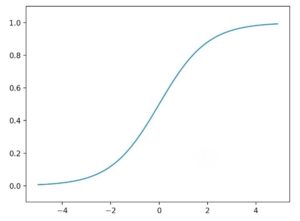
シグモイド関数の微分は最大値が0.25だから、
連鎖率の原理で微分が掛け算されると誤差ドンドン小さくなって、勾配消失問題が起きます（>_<）

そこで、Relu関数よく使われます。

Relu関数のは微分はxが0より大きい限り、常に1となるので勾配消失問題は発生しにくいのです。

出力層の活性化関数に必要な役割

出力層の活性化関数に必要な役割は「答えの形式を合わせる」ことです。

例えば…

[犬or猫or人]などの多値分類はソフトマックス関数

[大人or子供]などの２値分類はシグモイド関数

が有効です。

中間層・出力層で使用する活性化関数の種類

ディープニューラルネットワークの中間層か出力層のいづれに属するかによって、使用する活性化関数が異なります。中間層・出力層の其々で使用する活性化関数の種類をご説明します。

中間層の活性化関数

主に中間層で用いられる活性化関数です。

Relu関数

入力した値が0以下のとき0になり、1より大きいとき入力をそのまま出力します。

勾配消失問題が起こりにくい特徴を持ちます。

出力層の活性化関数

主に出力層で用いられる活性化関数です。

ソフトマックス関数

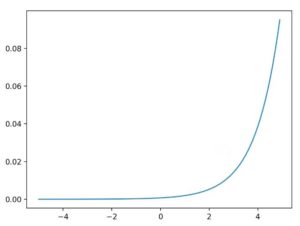
複数の出力値の合計が1.0（＝100％）になるように変換して出力します。

各出力値の範囲は0.0～1.0です。

[犬or猫or人]などの多値分類に用いられます。

シグモイド関数

入力値が大きいほど1に近づき、入力値が小さいほど0に近づくように変換して出力します。

[大人or子供]などの２値分類に用いられます。

恒等関数

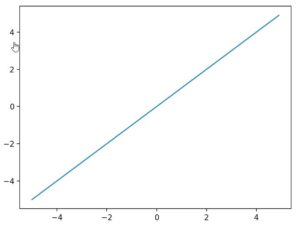
入力した値と同じ値を常にそのまま返します。

活性化関数の３つの目的！中間層と出力層で役割　まとめ

いかがでしょうか。

主に、活性化関数の種類や中間層・出力層で必要な理由についてご説明いたしました。

まとめますと…

活性化関数の第１の役割は、誤差を求めるために微分できること！

活性化関数はReluが中継ぎエースで抑えはシグモイドかソフトマックス！

です。

中継ぎ＝中間層、抑え＝出力層

で例えましたけど、余計にわかりにくかったかな…

理論を学ぶ事ってやっぱ重要やなぁって思います。

ワカランことだらけなので、まだまだ勉強です。

実は、この記事も活性化関数が中間層で必要な理由がわからなかったので調べた結果を書いたものです。

ＳＥおっさん

ここまで読んでくれてありがとう！

「記事を読んでもわからないトコがある」「内容が変だよ」
という時は、お気軽にコメントください♪

「もっとＳＥおっさんに詳しく聞きたい。何かお願いしたい！」
という時は、ココナラまで。メッセージもお気軽に♪

LINEでのお問合わせも受付中！
LINE公式アカウント

メッセージをお待ちしています！

Follow @koisyo_ok